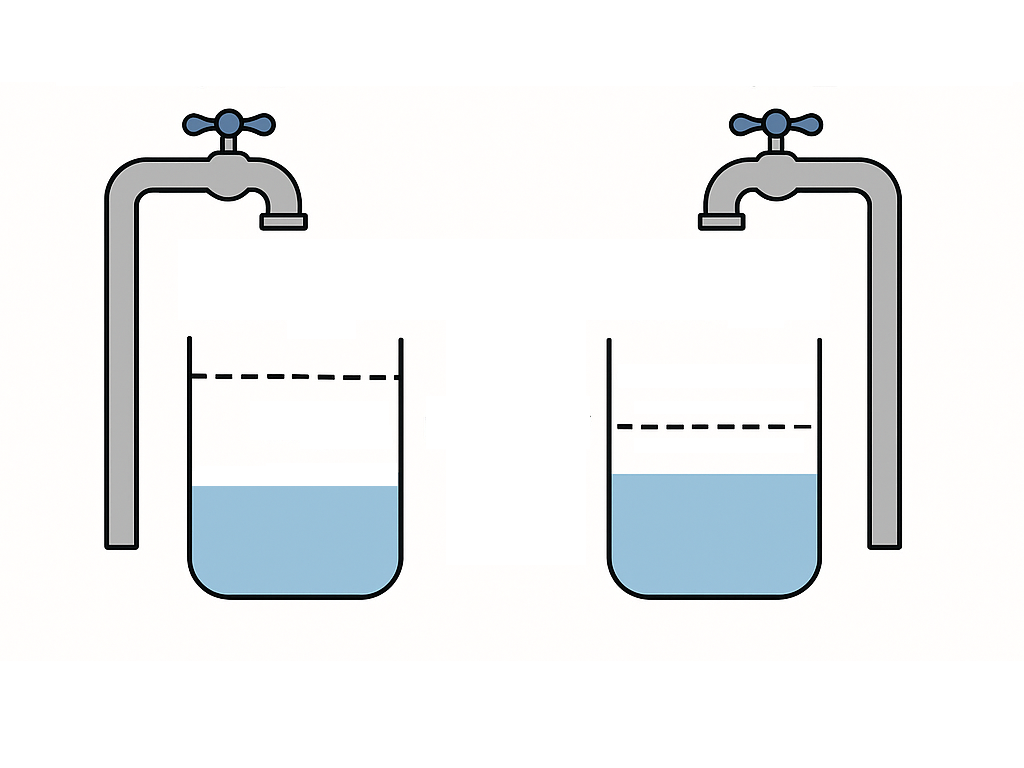
Welcome to Fill the Tank, a game of simultaneous decision-making under shared constraints. This game invites you to think about strategy, cooperation, and competition in dynamic systems with limited resources.
🎯Objective
Two players–![]() and
and ![]() –aim to fill their own tanks to a target volume, denoted as
–aim to fill their own tanks to a target volume, denoted as ![]() and
and ![]() , respectively. At each time step, they simultaneously adjust their taps to control the flow into their tanks, while trying not to exceed the shared maximum flow limit.
, respectively. At each time step, they simultaneously adjust their taps to control the flow into their tanks, while trying not to exceed the shared maximum flow limit.
The challenge is to reach their target volumes in as few steps as possible.
⚙️Game Structure
Each player has partial knowledge:
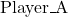 knows:
knows: 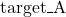 ,
, 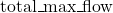 , and
, and 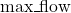
 knows:
knows: 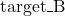 ,
, 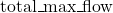 , and
, and 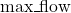
Time is discrete: ![]()
At each time step, both players simulatenously choose an action:
If the sum of these actions is within the allowed ![]() , then the flow is delivered. Otherwise, neither player receives flow at that step.
, then the flow is delivered. Otherwise, neither player receives flow at that step.
📏Game Rules
- Simultaneous Play: Both players choose their tap levels at the same time.
- Flow Limit: If
![Rendered by QuickLaTeX.com \mbox{action\_A}[k] + \mbox{action\_B}[k] > \mbox{total\_max\_flow}](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-057994b24bb221317aa764ec899d63dd_l3.png) , then both players receive no flow:
, then both players receive no flow:
- Otherwise, if within the limit:
- Tank Update:
- Score Update:
- Game Ends in Success: If
![Rendered by QuickLaTeX.com \mbox{vol\_A}[k] = \mbox{target\_A}](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-273e085f23bb199d0f2e741d552d8030_l3.png) and
and ![Rendered by QuickLaTeX.com \mbox{vol\_B}[k] = \mbox{target\_B}](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-318d1c2f01e9ba8d94536be6100b66f3_l3.png)
- Final Score:
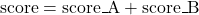
- Final Score:
- Game Ends in Failure: If either volume exceeds its target.
- Final Score:
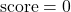
- Final Score:
- Penalty for Delay: If the game does not end at step
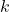 , score update:
, score update:
🧩Information Structure and Decision Process
Each player makes decisions based on partial knowledge and their own historical data.
 knows:
knows:
- Their own target volume
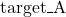
- The global limit
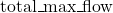
- The individual tap limit
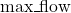
- Their own target volume
 knows:
knows:
- Their own target volume
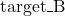
- The global limit
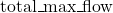
- The individual tap limit
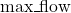
- Their own target volume
At each discrete time step ![]() , both players act simultaneously and independently, without access to the other player’s past actions or flow outcomes. Instead, they rely solely on their own information history:
, both players act simultaneously and independently, without access to the other player’s past actions or flow outcomes. Instead, they rely solely on their own information history:
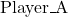 has access to:
has access to:
- Their past actions:
![Rendered by QuickLaTeX.com \mbox{action\_A}[0], \mbox{action\_A}[1], \dots, \mbox{action\_A}[k-1]](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-6f956928eb8fac663628a8023a9916ab_l3.png)
- Their received flow:
![Rendered by QuickLaTeX.com \mbox{flow\_A}[0], \mbox{flow\_A}[1], \dots, \mbox{flow\_A}[k-1]](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-443e3558aa53da6f05b1d75a8a7a09d8_l3.png)
- Their past actions:
 has access to:
has access to:
- Their past actions:
![Rendered by QuickLaTeX.com \mbox{action\_B}[0], \mbox{action\_B}[1], \dots, \mbox{action\_B}[k-1]](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-0a0f2fda20b86e49958ab54a3fe7eb85_l3.png)
- Their received flow:
![Rendered by QuickLaTeX.com \mbox{flow\_B}[0], \mbox{flow\_B}[1], \dots, \mbox{flow\_B}[k-1]](https://www.ahmettahakoru.com/wp-content/ql-cache/quicklatex.com-8ac867b997698e5f91b746f453006c0a_l3.png)
- Their past actions:
Players may choose to apply the same strategy or develop and apply different strategies.
The goal in all cases is to maximize the total score under varying conditions of ![]() and
and ![]() .
.
📊 Benchmarking Setup and Results
To evaluate strategies fairly, we propose a standardized benchmarking procedure. This allows researchers to compare different approaches on a common set of scenarios and assess their effectiveness.
⚙️ Benchmark Parameters
- Flow limits:
- Test Cases:
- We evaluate the performance of a strategy over all pairs:
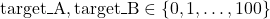
- This results in a total of 10,201 unique test cases
- We evaluate the performance of a strategy over all pairs:
- Execution:
- For each pair
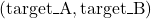 , both players apply the selected strategy (either the same or different).
, both players apply the selected strategy (either the same or different). - The game is simulated until termination: either successful completion or failure due to overshooting.
- The final score is recorded for each case.
- For each pair
📈 Performance Metric
Cumulative Score: The total sum of individual game scores across all 10,201 scenarios.
This metric reflects how well a strategy generalizes across a wide range of possible target configurations.
🎯 Goal
The benchmarking framework encourages development of strategies that are:
- Robust to asymmetry in targets
- Efficient in minimizing the number of steps
If you would like to submit a strategy for benchmarking or contribute benchmarking results using your own method, please reach out or comment to this page.
🧪 Example Strategy: Balanced Sharing Control
To get started, here is a simple yet effective baseline strategy that each player can implement independently
def strategy_sharing_half(vol, target):
missing_part = target - vol
action = min(missing_part, self.max_flow, math.floor(self.total_max_flow/2))
return actionThis strategy is based on a simple principle: before the game starts, both players agree not to exceed half of the total available flow (![]() ) to avoid conflicts.
) to avoid conflicts.
Note: While this strategy is simple and fair, it is not always efficient.
For example, in the case where ![]() and
and ![]() , Player_A may unnecessarily limit their actions by sticking to half of the total flow, even though Player_B needs much more. Smarter strategies can adapt to such imbalances and improve overall performance.
, Player_A may unnecessarily limit their actions by sticking to half of the total flow, even though Player_B needs much more. Smarter strategies can adapt to such imbalances and improve overall performance.
Using the benchmark settings, cumulative score of this strategy is 759,800.
💻 Reference Code
You can download the full source code from the GitHub repository:
🔗https://github.com/ahtakoru/fillthetank
The code is also available below:
import math
import itertools
class Game:
def __init__(self, max_flow = 10, total_max_flow = 10):
self.max_flow = max_flow
self.total_max_flow = total_max_flow
def reset(self, targetA, targetB):
self.done = False
self.scoreA, self.scoreB = 0, 0
self.volA, self.volB = 0, 0
self.targetA, self.targetB = targetA, targetB
self.history_actionA = []
self.history_actionB = []
self.history_flowA = []
self.history_flowB = []
def play_wo_print(self, targetA, targetB):
self.reset(targetA, targetB)
while self.done == False:
decisionA, decisionB, flowA, flowB = self.step()
return self.scoreA + self.scoreB
def play_with_print(self, targetA, targetB):
self.reset(targetA, targetB)
while self.done == False:
decisionA, decisionB, flowA, flowB = self.step()
print(f"Dec A: {decisionA} | Flow A: {flowA} | Vol/Tar A: {self.volA}/{self.targetA} |||| Vol/Tar B: {self.volB}/{self.targetB} | Dec B: {decisionB} | Flow B: {flowB} | ")
score = self.scoreA + self.scoreB
print(f"Total score: {score}")
return score
def step(self):
if not self.done:
# Replace with your strategy
actionA = self.strategy_sharing_half(self.volA, self.targetA)
actionB = self.strategy_sharing_half(self.volB, self.targetB)
# 0 <= flow <= each_max_flow
flowA = min(actionA, self.max_flow)
flowA = max(0, flowA)
flowB = min(actionB, self.max_flow)
flowB = max(0, flowB)
# flow constraint
if (flowA + flowB > self.total_max_flow):
flowA, flowB = 0, 0
self.history_actionA.append(actionA)
self.history_actionB.append(actionB)
self.history_flowA.append(flowA)
self.history_flowB.append(flowB)
self.volA += flowA
self.volB += flowB
self.scoreA += flowA
self.scoreB += flowB
score = self.scoreA + self.scoreB
if (self.volA == self.targetA) and (self.volB == self.targetB):
self.done = True
elif (self.volA > self.targetA) or (self.volB > self.targetB):
self.scoreA, self.scoreB = 0, 0
self.done = True
else:
self.scoreA -= 1 # Punishment for finishing late
self.scoreB -= 1 # Punishment for finishing late
self.done = False
return actionA, actionB, flowA, flowB
def strategy_sharing_half(self, vol, target):
missing_part = target - vol
action = min(missing_part, self.max_flow, math.floor(self.total_max_flow/2))
return action
def strategy_new(self, vol, target, history_action, history_flow):
pass
import os
if __name__ == "__main__":
os.system('cls')
game = Game()
# # Play a single game
# game.play_with_print(7,7)
# Test strategy
S = list(range(101)) # S = [0, 1, ..., 30]
target_list = itertools.product(S, S)
total_score = 0
for target in target_list:
score = game.play_wo_print(target[0], target[1])
total_score += score
print(f"target: {target} | score: {score}")
print(f"Strategy score: {total_score}")
🤝Call for Contributions
This game is intentionally open-ended to invite:
- 📚 Game-theoretic analysis: Equilibrium strategies, cooperative/competitive dynamics, payoff structures.
- 🧠 Algorithm design: Heuristics, optimization, reinforcement learning approaches.
- 📢 Community feedback: Share your thoughts, suggest rule variants, or propose theoretical extensions.
All interested researchers and engineers are warmly welcomed to contribute. If you develop strategies or analyses based on this game, please remember to credit me.
✍️How to Participate
- Submit your strategy or analysis via email
- Comment below or share feedback publicly
- Reach out to co-author publications or extensions
Let’s explore how intelligent strategies evolve under constraints — together.